함수 식 연립의 의미

함수 식을 '연립한다'라는 의미를 잘 이해하지 못하는 학생들이 많아요.

 

예를 먼저 들어볼게요. 아래의 두 함수가 있다고 해봅시다.

 

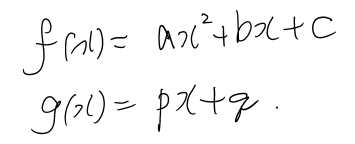
첫 번째 함수인 f(x) 그래프가 아래와 같다고 해볼게요.

 

x축과 같은 의미인 y=0과 f(x)를 연립한다면 이는 어떤 x값이 대입되었을 때 y=0도 만족하면서 f(x)위에 있을까? 라는 방정식이 돼요. 즉, f(x)의 함숫값이 0이 되도록 하는 x좌표는 어디인가? 가 되는 거죠. 답은 x절편의 x 좌표입니다.

여기서 흔히 적용하는 판별식을 적용하면 D>0이 됩니다. x축(y=0)과 만나는 점이 두 개니까요.

 

이제 f(x)와 g(x)를 연립해볼게요.

f(x)와 g(x)를 아래 그래프처럼 그려봅시다

f(x)=g(x)라고 둔다면, 어떤 x값이 들어갔을 때 f(x)의 값과, g(x)의 값이 같아지겠느냐? 라는 질문이 돼요.

즉, 두 함수의 교점을 구하는 거죠.

위 그래프로 보시면 아시겠지만 교점은 2개가 있어요.(빨간색으로 표시된 점)

두 교접의 x좌표값을 구하는 식은 아래와 같습니다. 많이 보셨을 거에요.

세번째 식에서 무턱대고 판별식을 적용하는 아이들이 많은데요, 여기서 판별식을 적용하는건 무슨 의미일까요?

맞아요. 앞서 이야기했듯 f(x)와 g(x)의 교점이 대체 몇 개일까? 라는 질문에 대한 답입니다.

직접 교점을 구해야하는 경우엔 판별식을 적용하는게 아니라 세번쨰 식을 직접 풀어야해요. 인수분해로 풀 수 있으면 좋겠지만, 아니면 근의 공식을 대입해야겠죠.

 

정리하자면, '서로 다른 두 함수를 연립한다' 라는건, 두 함수의 그래프 간의 교점의 x좌표를 구하겠다는 의미입니다.

교점의 y 좌표는 직접 함수 식에 대입해서 값을 계산하면 돼요. f(x)로 계산하든 g(x)로 계산하든 값은 같게 나올 겁니다.

 

기초적인 내용이지만, 도움이 되었길 바랍니다:)